V tomto článku se dozvíte, co je to:
- absolutní četnost
- relativní četnost
- validní četnost
- kumulativní četnost
Jednou ze základních analýz, které v marketingovém či jiném výzkumu využíváme, je analýza četností. Četnost udává počet, frekvenci opakování určité hodnoty v souboru. Jinými slovy četnost nám říká, kolik hodnot daného znaku se vyskytuje ve statistickém souboru. Z hlediska marketingového výzkumu nám analýza četností představuje tzv. třídění prvního stupně.
Rozlišujeme několik typů četností.
Absolutní četnost
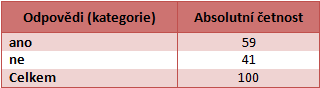
Udává sumu jednotlivých variant odpovědí, v číslech. Sečteme-li jednotlivé absolutní četnosti, dostaneme celkový počet hodnot v souboru. Absolutní četnosti nám neumožňují příliš věrohodně porovnávat dva soubory s různým počtem hodnot. Například na obrázku níže vidíme, že variantu odpovědi „ano“ zvolilo 59 ze 100 dotázaných a variantu „ne“ zvolilo 41 respondentů.
Relativní četnost
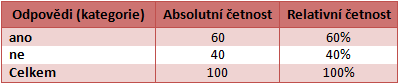
Ta udává poměrové rozložení odpovědí, tzn. jsou vyjádřeny v procentech a jejich součet se rovná 100 % (popř. 1, při vyjádření relativních četností desetinnými čísly). Je to počet hodnot v určitém intervalu vztažený k celkovému počtu hodnot. Výhodou je, že oproti absolutním četnostem, můžeme relativní četnosti využít k porovnávání více datových souborů různých velikostí (tzn. při procentním vyjádření, můžeme porovnávat četnosti například dvou souborů, z nichž první má celkem 100 hodnot a druhý třeba 140 hodnot). Relativní četnosti mají pro nás tudíž větší vypovídací hodnotu.
- soubor dat se 100 hodnotami
- soubor dat se 140 hodnotami
Validní četnost
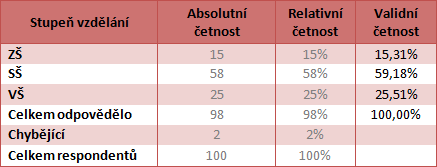
S validní četností počítáme v případě, že máme v datové matici nějaké chybějící hodnoty – tzn. že nám u některého statistického znaku chybí naměřené hodnoty (např. že některý respondent nebo respondenti na některou otázku z nějakého důvodu neodpověděli). V tabulce vidíme, že dva respondenti neodpověděli na otázku, čili počítáme validní četnosti, a jako základnu, jako celek bereme těch 98 lidí. Tzn. že validní četnosti jsou očištěny od chybějících hodnot.
Kumulativní četnost
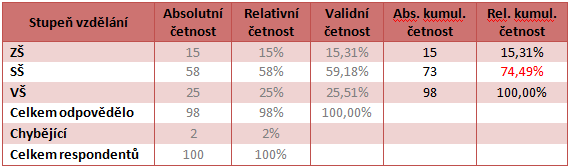
Můžeme je počítat z absolutních i relativních četností, nicméně nemůžeme je počítat u nominálních proměnných. Protože kumulativní četnosti nám postupně načítají jednotlivé absolutní nebo relativní četnosti, ať už sestupně nebo vzestupně. A jelikož nominální proměnné nemají logické pořadí, proto mají kumulativní četnosti smysl jen u ordinálních proměnných. Interpretace pak vypadá například takto (viz obrázek níže – ordinální proměnná vzdělání). Respondentů, kteří dosáhli nejvýše středoškolského vzdělání, je 74,49 %.
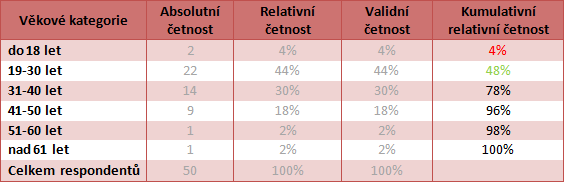
Nebo jiný příklad, máme věkové kategorie, viz obrázek níže – ordinální proměnná věkové kategorie. A můžeme říct, že jenom 4 % respondentů jsou mladší 18 let a téměř polovina respondentů je mladších 30 let. A tak dále. Ta procenta se zkrátka načítají, v tomto případě vzestupně.
Takže to byly četnosti na všechny způsoby. Ti z Vás, kteří znají statistický program SPSS, ještě možná využijí poznatky z tohoto videa: SPSS návod – četnosti (frequencies)


Facebook Comments